from __future__ import print_function
Precisione, Accuratezza e Velocità
Numeri in virgola mobile¶
Quando si parla di calcolo numerico si sente sempre parlare di "numeri in virgola mobile", ma cosa sono?! E, soprattutto, cosa hanno a che fare con i numeri "reali" con cui lavoriamo tutti i giorni?!
Alcune regole da tenere sempre a mente:¶
Dal momento in cui si mettono le mani su un computer bisogna dimenticarsi della parola continuo!
Ogni numero che esce da un computer sarà sempre finito ed un'approssimazione di un numero reale.
Il vantaggio nell'utilizzare numeri in virgola mobile sta nel fatto che possiamo accedere ad un più ampio range di valori (es. sistema a 64 bit):
- int: -2,147,483,648 a +2,147,483,647
- float: 1.4 $\times 10^{-45}$ a 3.4 $\times 10^{38}$
- double: $\sim10^{-323}$ a $\sim10^{308}$
Ma soprattutto:¶
Più operazioni si fanno e più informazioni numeriche si perdono.
Più righe di codice si scrivono e più errori è facile commettere.
Bene...una cosa per volta...
Cominciamo dai numeri...
Floating-Point Numbers¶
Un numero cosiddetto "in virgola mobile" è una rappresentazione approssimata di un numero reale.
Questa approssimazione è necessaria per descrivere numeri che risulterebbero troppo grandi/piccoli per essere rappresentati come interi.
Senza andare troppo nel dettaglio vi basti sapere che...
...un numero all'intero del calcolatore deve essere inevitabilmente rappresentato.
Per farlo scomponiamo il numero in 3 parti:
- un campo denominato mantissa M
- un campo esponente e
- ed un bit di segno s
In questo modo un numero sarà rappresentato da
$n = (-1)^s \times M \times 2^e$
Precisione e round off¶
Essendo i numeri floating-point solamente delle approssimazioni dei numeri reali ogni tanto possiamo avere qualche problema di rappresentazione. Ad esempio:
- numeri irrazionali ($\sqrt{2}$, $\pi$)
- numeri non rappresentabili (0.1)
- round-off dovuto ad operazioni (2/3 = 0.66667 )
- ecc.
Si va bene ma cosa vuol dire?
Ad esempio?
print ("%f = %.32f"%(0.1, 0.1)) #scrittura del numero 0.1 con 32 cifre decimali
print ("%.17f + %.17f = %.17f"%(0.1,0.2,0.1 + 0.2))
print (0.1)
Remember, remember...¶
Python, come anche Matlab, lavora con 53 bit di precisione e quindi i valori che ha al suo interno non sono quelli che ci fa vedere con un semplice "print".
cit.
"If Python were to print the true decimal value of the binary approximation stored for 0.1, it would
have to display <0.1000000000000000055511151231257827021181583404541015625> that is more digits than
most people find useful."Aritmetica Floating-Point¶
L'aritmetica dei numeri floating-points non è equivalente a quella dei numeri reali:
- associativa(+) : $(x+y)+z \neq x + (y+z)$
- associativa($\times$) : $(x \times y) \times z \neq x \times (y \times z)$
- distributiva : $x \times (y+z) \neq (x \times y)+(x \times z)$
- round : $x + \epsilon - x \neq \epsilon$
- division : $a/b \neq a \times (1/b)$
- algorithms : $(a+b) \times (a-b) \neq a^2-b^2$
- ecc.
a = 0.1
b = 0.2
c = 0.3
print ((a + b) + c, a + (b + c))
assert((a + b) + c == a + (b + c)) #verifica della proprietà associativa(+) considerando tutti i bit
Floating-Points exceptions¶
Oltre ai problemi di precisione e round-off lo standard floating point IEEE definisce alcune eccezioni che possono insorgere durante il calcolo.
Underflow : avviene quando il risultato di un'operazione è troppo piccolo per essere rappresentato.
Overflow : avviene quando il risultato di un'operazione è troppo grande per essere rappresentato.
Divide-by-zero : avviene quando si tenta di dividere un numero per zero.
Invalid : avviene quando un'operazione è mal-definita (es. (0.0 / 0.0).
Inexact : avviene quando il risultato di un'operazione non è esatto, i.e. il risultato è arrotondato.
Precisione, Accuratezza e Velocità
Scelta dell'algoritmo¶
Ci sono tanti modi diversi per fare la stessa operazione.
Scegliere l'algoritmo migliore per ogni evenienza è un'arte (strettamente correlata con l'esperienza!)
Per capirci meglio facciamo qualche prova...
Prendiamo il calcolo dell'inverso della radice quadrata di un numero:
$$ \frac{1}{\sqrt{x}} $$Chiunque (sfido il contrario!) utilizzerebbe la formula esattamente com'è scritta!
import numpy as np
print (1./np.sqrt(4))
MA...¶
Qualcuno (non so davvero chi...decisamente me incluso) potrebbe pensare di calcolarla sviluppando il rapporto come:
def isqrt(number):
assert number > 0
threehalfs = 1.5
x2 = number * 0.5
y = np.float32(number) #conversione a float32 del numero
i = y.view(np.int32) #"vedi" y come una variabile int32
i = np.int32(0x5f3759df) - np.int32(i >> 1) #differenza tra numeri in bit-format
y = i.view(np.float32)
y = y * (threehalfs - (x2 * y * y))
return float(y)
print (isqrt(4))
Più complesso non è sempre peggio...se ben pensato!¶
Questo secondo algoritmo, noto come Fast inverse square root è uno degli algoritmi più noti e rivoluzionari degli ultimi anni.
La matematica che ci sta dietro è relativa ad un algoritmo iterativo di Newton che consente di convergere ad una soluzione approssimata e molto veloce di $1/\sqrt{x}$.
Un esempio più comune¶
Supponiamo di voler calcolare il valore medio di un vettore $x$. Saremo tutti d'accordo che questo sia calcolabile come:
$E[x] = \sum_{i=1}^N \frac{x_i}{N}$
che è certamente equivalente a
$E[x] = \frac{1}{N}\sum_{i=1}^N x_i$
Bene...proviamo allora
import numpy as np
N = 10000
x = np.random.rand(N) #vettore contenente N numeri random estratti uniformemente in [0,1]
mean_1 = 0.0
mean_2 = 0.0
for x_i in x:
mean_1 += x_i / N
mean_2 += x_i
mean_2 /= N
print ("Media 1 = %.32f"%(mean_1))
print ("Media 2 = %.32f"%(mean_2))
Cost of Operations¶
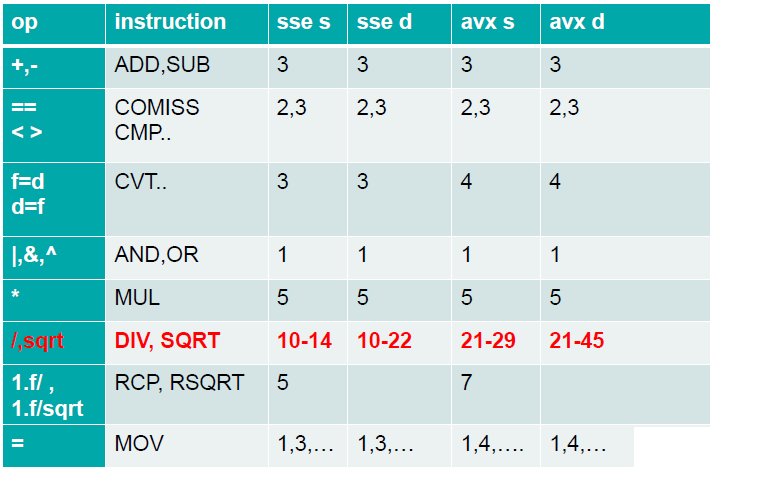
Cost of Functions¶

Precisione, Accuratezza, Velocità
Cosa vuol dire velocità di un codice¶
Ci sono molti modi per velocizzare ed ottimizzare un algoritmo ed ognuno di essi è adatto per una problematica differente.
- Ottimizzazione degli accessi alla memoria.
- Parallelizzazione del codice.
- Vettorizzazione.
Come si capisce dal nome la vettorizzazione si applica a strutture di tipo vettore e/o matrice.
L'idea fondamentale dietro questa "tecnica" di programmazione è quella di applicare l'operazione che verrebbe eseguita su ciascun elemento di un vettore a tutti gli elementi di quest'ultimo...insieme!
In poche parole il paradigma:
Single Instruction Multiple Data¶
Ad esempio¶
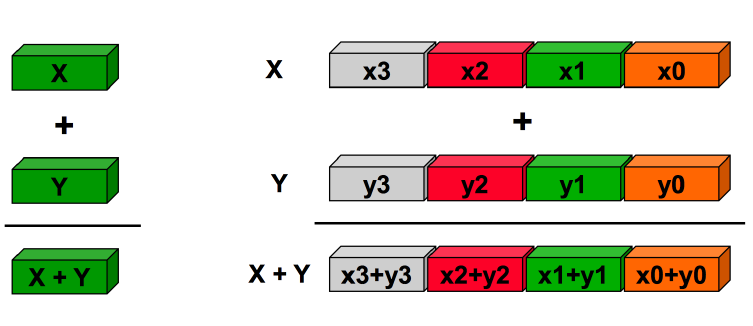
Quindi...
- Abbiamo bisogno di un Loop.
- Dobbiamo trasformare questo loop in N streams.
- Ogni iterazione del loop deve essere eseguita!!(*)
NOTA: la vettorizzazione di un loop è uno dei metodi più rapidi da implementare e con il miglior guadagno in tempi di calcolo...soprattutto nei linguaggi ad alto livello!
print ('true' if True else 'false') # operatore ternario del C++ in Python: la sintassi è "output1 se condizione, altrimenti output2
print ('false' if False else 'false')
print ('odd' if 5%2 else 'even')
print ('odd' if 4%2 else 'even')
NumPy - Numerical Python¶
NumPy è la libreria fondamentale per il calcolo scientifico ad alte performance e l'analisi di dati.
Gli oggetti messi a disposizione dalla libreria presentano tutti i più comuni algoritmi già implementati con metodi vettorizzati, nonché tool per la lettura/scrittura di dati da disco, algebra lineare e, perché no, anche la possibilità di wrappare codici C++ all'interno di Python!
Una buona guida, oltre al Reference di Numpy stesso, la potete trovare all'indirizzo https://www.safaribooksonline.com/library/view/python-for-data/9781449323592/ch04.html (a cui anche io mi sono ispirato per i prossimi esempi)
I NumPy array e ndarray¶
Proprio come gli std::vector
import numpy as np
a = np.array([1,2,3,4]) # vettore 1x4
print ("a = ", a)
b = np.array([[1,2,3,4],[5,6,7,8]]) # matrice 2x4
print ("b = ", b)
Ogni array ha a disposizione numerose funzioni:
- array.shape : ritorna la dimensione dell'array
- array.dtype : ritorna il tipo di dato contenuto
- len(array) : ritorna la dimensione delle righe di una matrice o più in generale la prima dimensione dell'ndarray.
- np.array(lista) o np.array(tupla) : converte in un numpy array l'oggetto.
a = [1,2,3,4]
a_array = np.array(a)
b_array = np.asarray(list(a))
print (a_array.shape)
print (b_array.shape)
print (a_array.dtype)
print (len(a_array))
Creare array¶
Ci sono 3 funzioni importanti per la creazione di array e l'inizializzazione di array.
array_zeros = np.zeros(10) # vettore 1x10 di zeri
print ("array_zeros = ", array_zeros)
print ("array_zeros ha dimensioni : ", array_zeros.shape)
a_matzeros = np.zeros((2,10)) # matrice 2x10 di zeri
print ("a_matzeros ha dimensioni : ", a_matzeros.shape)
array_ones = np.ones(10) # vettore 1x10 di uno
print ("aarray_ones = ", array_ones)
a_empty = np.empty(20) # vettore 1x20 di valori "vuoti"=locazioni di memoria libere
print ("a_empty = ", a_empty)
print ("a_empty contiene oggetti di tipo : ", a_empty.dtype)
Attenzione¶
Non è sicuro assumere che oggetti di tipo np.empty contengano valori nulli!!
In molti casi infatti contengono solamente "sporcizia" di memoria.
Altri tipi di inizializzazione¶
Posso anche creare array che contengano numeri appartenenti ad un range numerico crescente o decrescente.
Le principali funzioni sono 2: np.arange e np.linspace
a = np.arange(10) # vettore di 10 elementi con numeri crescenti da 0(default) e 10
print (a)
a = np.arange(1, 10, 2) # (valore iniziale, valore finale, step)
print (a)
a = np.linspace(0, 2, 4) # (valore iniziale, valore finale, numero di punti)
print (a)
a = np.array([1,2,3,4], dtype=np.float64)
print ("a = ", a)
print ("a contiene elementi di tipo : ", a.dtype)
a = np.array([1,2,3,4], dtype=np.uint32)
print ("a = ", a)
print ("a contiene elementi di tipo : ", a.dtype)
a = np.array(['1.21', '.2', '-.4'], dtype = np.string_)
print ("a di stringhe = ", a)
print ("a cast 2 float = ", a.astype(np.float64))
Operazioni tra Arrays e Scalari¶
I NumPy array non sono solo belli da vedersi ma ci tolgono anche tanti pensieri sul calcolo numerico e algebrico...
...ma soprattutto hanno tutta una serie di operazioni già vettorizzate!!
a = np.array([1,2,3,4])
b = np.array([2,3,4,5])
print ("\n OPERAZIONI ARITMETICHE\n")
print ("a = ", a)
print ("b = ", b)
print ("a * 10 : ", a * 10)
print ("a + 2 : ", a + 2)
print ("a^2 : ", a**2)
print ("\n OPERAZIONI TRA ARRAY\n")
print ("a * b : ", a*b)
print ("a + b : ", a+b)
print ("a - b : ", a-b)
print ("1. / a : ", 1./a)
print ("1 / a : ", 1/a)
Posso anche prendere pezzi dei vettori e combinarli insieme.
a = np.arange(20)
print (a)
print (a[8]) # ottavo elemento del vettore
print (a[:8]) # primi 8 elementi
print (a[8:12]) # elementi compresi tra l'ottavo e il dodicesimo
print (a[12:-4]) # elementi compresi tra il 12esimo e il quart'ultimo
print (a[-4:]) # elementi dal quart'ultimo e la fine
assert( np.all(a[-15:-10] == a[5:10]))
ATTENZIONE!¶
a = np.arange(10)
print (a)
arr_slice = a[2:5] # pezzo del vettore a
arr_slice[1] = 10000 # modifica del secondo elemento del pezzo di a
print (a)
Quando volete copiare una porzione di un array senza che le modifiche si ripercuotano sull'array originale dovete usare il comando appropriato...che con grande fantasia sarà
arr[2:5].copy()arr3d = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
print (" a = ", arr3d)
print ("primo elemento : ", arr3d[0][0][0])
print ("prima riga : ", arr3d[0][0])
print ("prima matrice : ", arr3d[0])
print ("profondità : ", arr3d[:, 0, 0])
Torniamo all'esempio di prima...¶
Vediamo di quantificare un po' i guadagni di tempo legati alla vettorizzazione.
NumPy mette a disposizione una sua versione vettorizzata del calcolo della media di un vettore
np.mean(array)import time
start_time = time.time() # inizia a contare il tempo
N = int(1e7)
x = np.random.rand(N)
mean_for_1 = 0.0
mean_for_2 = 0.0
for x_i in x:
mean_for_1 += x_i/N
mean_for_2 += x_i
mean_for_2 /= N
print ("Mean 1 = %.32f"%(mean_for_1))
print ("Mean 2 = %.32f"%(mean_for_2))
print ("Calcolate in %.32f sec"%(time.time()-start_time))
start_time = time.time()
mean_vec = np.mean(x)
print ("Mean vettorizzata = %.32f"%(mean_vec))
print ("Calcolata in %.32f sec"%(time.time()-start_time))
Random numbers¶
Una classe di funzioni molto importante per la programmazione è la generazione di numeri random.
Numpy predispone già un'ampia gamma di generatori!
from numpy import random
print (random.rand()) # uniform distribution
print (random.randn()) # normal distribution
print (random.exponential()) # exponential distribution
print (random.rand(2, 3)) # random matrix
Una carrellata di altre funzioni utili...¶
NOTA In Matlab la nomenclatura è quasi sempre la stessa, ovviamente senza l'np davanti!
a = np.array([1, -2, 3.444, -2, 4.29, 6.98])
b = np.array([2, -2, 3.44, -2., 5, 7])
print ("\n ALCUNE altre operazioni \n")
print (np.abs(a)) # absolute value
print (np.fabs(a)) # absolute value
print (np.sqrt(a)) # square root
print (np.floor(a)) # the largest integer value less than or equal to x
print (np.ceil(a)) # smallest integer value greater than or equal to x
print ("a = ", a)
print ("b = ", b)
print ("\n ALCUNE operazioni logiche \n")
print (np.logical_and(a, b)) # AND
print (np.logical_or(a, b)) # OR
print (np.greater(a, b)) # >
print (np.equal(a, b)) # ==
print ("a = ", a)
print ("b = ", b)
print ("\n ALCUNE operazioni sul posizionamento \n")
print (np.sort(a)) # SORTING ELEMENTS
print (np.argsort(a)) # SORTING INDICES
print (np.where(a < 2)[0]) # INDICES WHERE CONDITION
print (np.where(a > 2, 1, 0)) # (CONDITION, IF(CONDITION), ELSE)
print (np.median(a)) # MEDIAN
Per tutto il resto...¶
Per ogni altra funzione vettorizzata che voi vogliate scrivere (ricordandovi quali sono le condizioni per vettorizzare un ciclo!) esiste la funzione
vectorized_func = np.vectorize(func) || bsxfun(func, input_func)
da applicare ad una funzione come
print vectorized_func(input_func)Basta teoria! E' ora di sporcarsi un po' le mani scrivendo del codice!¶
Da quello che abbiamo imparato dovreste essere in grado di vettorizzare facilmente il codice seguente per il calcolo del $\pi$. Controllate anche il tempo di esecuzione delle due versioni dell'algoritmo!
import numpy as np
import time
"""
Metropolis Algorithm
Algoritmo per il calcolo dell'integrale di una funzione attraverso un campionamento Monte Carlo.
In questo esempio viene utilizzato per il calcolo del valore del pi-greco. Si consideri al proposito un cerchio di
raggio unitario (r = 1) centrato nell'origine, inscritto in un quadrato. In questo modo il quadrato avrà lato pari a 2
e la sua area sarà uguale a 4. Andando ad estrarre in modo uniforme nell'intervallo [-1,1] una coppia di numeri (x, y),
qualora le coordinate risultino appartenenti al cerchio verrà conteggiato un Hit. La condizione da imporre sarà quindi:
x^2 + y^2 < 1
Secondo la teoria dei metodi Monte Carlo, il numero di Hit rispetto al totale sarà equivalente (per un numero tendente
all'infinito di estrazioni) al rapporto tra le aree. In questo caso quindi
Hit/Tot = pi/4
Volendo estrarre un risultato più robusto si consiglia di campionare il valore di pi un numero N_runs di volte, in modo
che il corretto valore di pi sia dato dalla media della distribuzione di più campionamenti Monte Carlo.
"""
N = 100000 # number of MC events
N_run = 100 # number of runs
Nhits = 0.0 # number of points accepted
pi = np.zeros(N_run) # values of pi
start_time = time.time() # start clock
for I in range(N_run):
Nhits = 0.0
for i in range(N):
x = np.random.rand()*2-1
y = np.random.rand()*2-1
res = x*x + y*y
if res < 1:
Nhits += 1.0
pi[I] += 4. * Nhits/N
run_time = time.time()
print ("pi with ", N, " steps for ", N_run, " runs is ", np.mean(pi), " in ", run_time-start_time, " sec")
print ("Precision computation : ", np.abs(np.mean(pi)-np.pi))